Multiscale modeling of concrete structures via localized model order reduction.
Source: BAM
Starting point: Computational Cost of Multiscale Simulations of Heterogeneous Materials
Every material is intrinsically multiscale, and - depending on the application - simulation models in science and engineering are required to fully resolve the finer scales in the numerical model. With significant variations present in spatial scales, the assumption a homogeneous material proves to be insufficient for analysis. For example, the aggregates dispersed in a cement matrix may lead to fluctuations in the displacement field which cannot be captured by a phenomenological macroscale model. However, the resolution of the heterogeneous fine scale features drastically increases the computational cost entailed with the direct numerical solution of the problem via e.g. finite element methods. Thus, new high-performance computational methods are required for multiscale simulations of large scale concrete structures.
Full Fine Scale Simulations Enabled Through Localized Model Order Reduction (MOR)
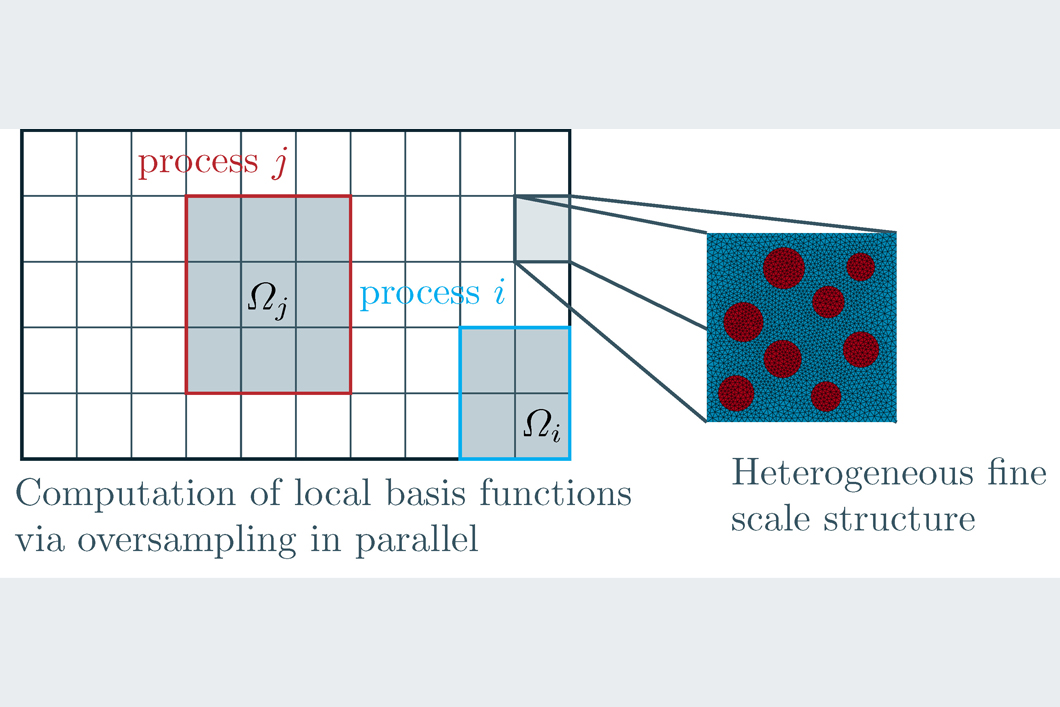
A promising approach to cope with the drastic increase in computational cost are MOR techniques. The original full order model (FOM) is replaced by a fast-to-evaluate reduced order model (ROM). The key point is the pre-computation of specialized global ansatz functions. These so-called reduced basis functions already contain essential information about the sought solution in the entire domain and enable to construct the ROM by projection of the FOM onto the low-dimensional subspace that is spanned by the reduced basis. However, the construction of the reduced basis is usually done using the FOM which is too costly to evaluate in the context of full fine scale simulations. The reduced basis functions can be calculated in a local manner, i.e. for only some part of the global domain, using the concept of oversampling to overcome this issue.
Physically Meaningful Random Samples in the Context of Oversampling
The oversampling problem consists in extending the domain around a small area of interest for which local reduced basis functions should be computed. This boundary value problem is then solved repeatedly with random boundary conditions to construct the reduced basis. The key contribution of our work is enhancing this procedure with a sampling strategy that includes physically meaningful correlated random samples in the training. The result is a reduced basis of high quality, that is able to approximate the true solution sufficiently well.
Multiscale modeling of linear elastic heterogeneous structures via localized model order reduction
Philipp Diercks, K. Veroy, Annika Robens-Radermacher, Jörg F. Unger
published in International Journal for Numerical Methods in Engineering, 2023, pages 1 bis 23.
BAM Department Safety of Structures
BAM Division Modelling and Simulation


